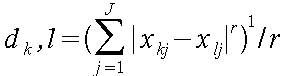Grundlagen[]
Das Ziel der Clusteranalyse ist die Unterteilung einer Menge von Objekten in Gruppen – die sogenannten Cluster. Die einem Cluster zugeordneten Objekte sollen sich dabei möglichst ähnlich sein (homogen), die unterschiedlichen Clustern zugeordneten Objekte sollen sich dagegen möglichst stark voneinander unterscheiden (heterogen). Die Besonderheit des Verfahrens ist, dass mehrere Merkmale parallel zueinander zur Clusterbildung herangezogen werden können, sich die Betrachtung der „Ähnlichkeit“ oder „Unähnlichkeit“ von Objekten also über mehrere Dimensionen erstreckt.
Genau darin liegt auch die theoretische Herausforderung des Verfahrens: Die „Ähnlichkeit“ von Objekten muss genau genug gemessen werden können, um zu einer Einteilung in Cluster zu gelangen. Es wird ein Verfahren benötigt, mit dem sich eine Kombination aus Merkmalsausprägungen für ein Objekt mit einer ebensolchen Kombination für ein anderes Objekt vergleichen lässt. Das bestmögliche Verfahren hierfür ist die hierarchische Clusteranalyse. Es erfordert nur geringfügige Voraussetzungen und ist daher fast in jeder Situation anwendbar – der Informationsgehalt des Ergebnisses ist dafür aber auch geringer als der anderer multivariater Analyseverfahren (z.B. Varianzanalyse, Faktorenanalyse).
Methodik[]
Bei der Clusteranalyse kommt die sogenannte „Methodik des hierarchischen Agglomerierens“ zum Einsatz. Diese Methodik umfasst mehrere Schritte, die mehrfach in einer Schleife durchlaufen werden.
Zunächst wird jedes vorhandene Objekt als einzelner Cluster betrachtet. Die beiden Cluster – auf dieser Stufe also noch die beiden Einzelobjekte – zwischen denen die geringste Distanz besteht – die sich also am ähnlichsten sind – werden miteinander vereinigt. Diese Vereinigung reduziert also die Anzahl der insgesamt vorhandenen Cluster um Eins. Für die noch vorhandenen Cluster werden anschließend erneut alle möglichen Distanzen berechnet und es kommt wieder zu einer Vereinigung der Objekte mit dem geringsten Abstand (gemessen werden muss also die Distanz zwischen zwei Einzelobjekten, die Distanz zwischen zwei Clustern und die Distanz zwischen Clustern und Einzelobjekten). Dieses Verfahren wird so lange fortgesetzt, bis alle Objekte in einem einzigen, großen Cluster vereinigt sind.
Dieser „Megacluster“ ist natürlich nicht als Endergebnis der Clusteranalyse zu betrachten. Statt dessen werden nun die Teilschritte untersucht, die zur Bildung dieses Megaclusters geführt haben. Die Teilstufe mit der am sinnvollsten erscheinenden Clusterung kann dann als Endergebnis selektiert werden, wobei hier viel interpretatorisches Geschick des Marktforschers gefragt ist.
Voraussetzungen[]
Für eine sinnvolle Clusteranalyse muss die Ähnlichkeit zweier Objekte mathematisch quantifizierbar sein. Metrisch skalierte Merkmale können daher problemlos in eine Clusteranalyse einfließen, ordinal und nominal skalierte Merkmale müssen dagegen als Dummy-Variablen codiert werden. Die gleichzeitige Verwendung metrischer und nichtmetrischer Merkmale in einer Clusteranalyse ist gestattet.
Zu bedenken ist auch, dass in unterschiedlichen Dimensionen skalierte Merkmale zu einer Ergebnisverzerrung führen. Wird beispielsweise eine Clusteranalyse mit den Merkmalen Alter und Einkommen durchgeführt, so werden sich bei den Einkommenswerten größere Abstände zwischen den Objekten zeigen. Dies wiederum hätte zur Folge, dass das Einkommen die Wertung der Ähnlichkeit/Unähnlichkeit viel stärker beeinflussen würde als das Alter. Um dieses Problem zu umgehen, können die Werte vor der Durchführung einer Clusteranalyse standardisiert werden – in der Regel durch eine Z-Transformation. Eine solche Transformation darf aber nicht durchgeführt werden, wenn keine unterschiedlich dimensionierten Werte vorliegen – hier muss der Marktforscher also aufpassen.
Die letzte Voraussetzung besteht darin, dass die zur Clusterbildung genutzten Merkmale nicht untereinander korrelieren sollten. Der Grund dafür ist, dass solche Korrelationen die Bedeutung der betroffenen Merkmalsgruppen verstärken, was leicht eine inhaltliche Fehlinterpretation der gefundenen Cluster nach sich zieht.
Distanzmaße[]
Distanzmaße dienen der Bestimmung der Distanz zwischen zwei Einzelobjekten. Die Grundlage für die Distanzmessung bildet die sogenannte Minkowski-Metrik:
Die entscheidende Größe in dieser Gleichung ist die Minkowski-Konstante r, mit der die Art der Minkowski-Metrik festgelegt wird. Dabei ist zu beachten, dass es sich bei Minkowski-Metriken grundsätzlich um Unähnlichkeitsmaße handelt, d.h. je größer das Maß, desto unähnlicher sind sich die Objekte.
Für metrische Daten sind vor allem vier Distanzmaße von Bedeutung:
- Euklidischer Abstand (bei r = 2)
- Quadrierter euklidischer Abstand
- Block-Distanz/Manhattan-Distanz (bei r=1)
- Tschebyscheff-Distanz
Für nichtmetrische Daten existieren sechs wesentliche Distanzmaße:
- Dice
- Jaccard
- Tanimoto
- Kulczynski
- Russel and Rao
- Simple Matching
Clustermethoden[]
Die Clustermethoden dienen der Bestimmung der Distanz zwischen zwei Clustern oder einem Cluster und einem Einzelobjekt. Hier sind fünf Methoden üblich, die nachfolgend jeweils kurz betrachtet werden sollen.
Linkage zwischen den Gruppen: Hier werden alle Paare konstruiert, die aus jedem der beiden Cluster je ein Objekt enthalten. Für jedes dieser Paare wird anhand der Distanzmaße auf die übliche Art die Distanz bestimmt. Das arithmetische Mittel aller aufgetretenen Distanzen wird dann als Distanz zwischen den Clustern gewertet.
Linkage innerhalb der Gruppen: Hier werden alle Paare konstruiert, die sich insgesamt aus den Objekten beider Cluster bilden lassen – also auch Paare, bei denen beide Objekte im gleichen Cluster liegen. Analog zum vorangegangenen Verfahren wird wieder das arithmetische Mittel aller aufgetretenen Distanzen als Distanz zwischen den Clustern gewertet.
Nächster Nachbar: Es wird das Paar aus Objekten beider Cluster gesucht, welches die kürzeste Distanz aufweist. Diese Distanz wird dann als Distanz zwischen den Clustern gewertet.
Entferntester Nachbar: Es wird das Paar aus Objekten beider Cluster gesucht, welches die größte Distanz aufweist. Diese Distanz wird dann als Distanz zwischen den Clustern gewertet.
Zentroid-Clustering: Hier entspricht die Distanz zwischen den Clustern der Distanz zwischen den beiden Objekten, die sich aus den jeweiligen arithmetischen Mitteln aller Objekte in den einzelnen Clustern errechnen.
Ward-Methode: Variablenmittelwerte des neuen Cluster ermitteln. Dann werden die Distanzen der einzelnen Objekte (aller) zu den Clustermittelwerten aufsummiert. Zusammenfassung der Objekte, bei denen der Zuwachs der Gesamtsumme aus den Distanzen am geringsten ist.
Auswertung und Clusterfindung[]
Die Ergebnisse einer Clusteranalyse werden dem Marktforscher in Form von zwei tabellarischen Darstellungen und zwei Grafiken präsentiert, deren Interpretation nachfolgend kurz betrachtet werden soll.
Die Distanzmatrix zeigt die Distanzwerte sämtlicher möglichen Einzelobjekt-Paare und damit gewissermaßen die Ausgangssituation vor dem ersten Schritt der Clusteranalyse. Sie ist symmetrisch aufgebaut, d.h. jeder Wert ist zweifach vorhanden, weshalb es ausreicht, die halbe Distanzmatrix zu betrachten.
Die Agglomerationstabelle zeigt den schrittweisen Verlauf der Clusteranalyse. In der ersten, obersten Stufe bildet jedes Objekt noch einen einzelnen Cluster, in der letzten, untersten Stufe sind alle Objekte in einem Megacluster vereint. Jede Zeile der Tabelle beschreibt somit genau einen Schritt der Clusterbildung (welcher Cluster bzw. welches Objekt wurde mit welchem anderen Cluster oder Objekt vereinigt?), wobei zu erkennen ist, dass die Distanzwerte (Koeffizienten) zwischen den vereinigten Objekten – also die bei der Vereinigung zu überbrückende Distanz – im Verlauf des Verfahrens beständig ansteigt. Dies ist typisch für die Clusteranalyse, da ja auch immer unähnlichere Objekte vereinigt werden, je näher das Verfahren der Bildung des Megaclusters kommt. Ein großer Sprung in den Koeffizienten kann als Hinweis darauf betrachtet werden, dass die finale Clusterbildung zwischen diesen beiden Vereinigungsstufen enden sollte.
Das Eiszapfendiagramm stellt den Prozess der Clusterbildung grafisch dar und gibt somit die gleichen Informationen wieder, wie die oben angesprochene Tabelle der Agglomerationsschritte – allerdings bei besserer Übersichtlichkeit. Von oben nach unten gelesen beschreibt also auch dieses Diagramm den schrittweisen Ablauf der Clusteranalyse, wobei sich in der untersten Stufe die Ausgangssituation und in der obersten Stufe der Megacluster findet.
Einen ähnlichen Informationsgehalt besitzt auch das 'Dendrogramm', welches wie das Eiszapfendiagramm den Ablauf der Clusteranalyse grafisch darstellt. Das Dendrogramm vereinigt dabei wichtige Informationen aus der Tabelle der Agglomerationsschritte (Entfernung der Cluster oder Einzelobjekte voneinander zum Zeitpunkt der Vereinigung) mit der grafischen Übersichtlichkeit des Eiszapfendiagramms, weshalb es diejenige Ergebnisgrafik ist, anhand der in der Regel die finale Einteilung der Objekte in die Cluster vollzogen wird. Da die Abstände zwischen den Objekten oder Clustern bei der Vereinigung direkt erkennbar sind, kann der Marktforscher sofort ablesen, ob es sich um eine Vereinigung noch relativ homogener oder bereits relativ heterogener Objekte oder Cluster handelt.
Zu beachten ist, dass in keinem Fall eine einzige, „richtige“ Clustereinteilung existiert, sondern in der Regel mehrere Clustereinteilungen Sinn machen. Bei der finalen Entscheidung sind sowohl die Erfahrung und das interpretatorische Geschick des Marktforschers als auch gegebenenfalls die Unterstützung durch entsprechende Fachexperten gefragt.
Quellen[]
C. Reinboth: Multivariate Analyseverfahren in der Marktforschung, LuLu-Verlagsgruppe, Morrisville, 2006.
Fahrmeir, L., Künstler, R., Pigeot, I. & Tutz, G. (1999). Statistik. Der Weg zur Datenanalyse (2. Aufl.). Berlin: Springer.
Brosius, F. (2002). SPSS 11. Bonn: mitp-Verlag.
Hair, J.F., Anderson, R.E., Tatham, R.L. & Black, W.C. (1998). Multivariate data analysis (5th ed.). Upper Saddle River, NJ: Prentice Hall.
Janssen, J. & Laatz, W. (2003). Statistische Analyse mit SPSS für Windows (4. Aufl.). Berlin: Springer.